Sensitivity Sensationalism

Loudspeaker sensitivity and power ratings have become the primary specifications used to design sound systems in cinema. This practice and these specifications are accepted at face value and not often questioned. They make designing sound systems fairly easy and straightforward. However, they rely on many assumptions and some of them are simply not valid, at least not to the absolute level ascribed to them. Easy answers to complex problems are rarely the correct ones.

The following assumptions must be true for current practices to be correct:

• The sensitivity of a loudspeaker with 1 watt input measured at 1 meter is accurately specified and can be used without question in calculating power requirements to achieve the desired SPL at all frequencies.
• The loudspeaker is a perfectly linear device. The corollary to this is that the speaker will still sound good at its full rated power.
• That leads to the assumption that amplifier power in dBW can be added to the 1W/1m sensitivity spec to determine the maximum SPL at 1 meter at all frequencies.
• The inverse square law can be used to determine the sound level at any given distance from a speaker. The assumption is that the sound level drops 6 dB for every doubling of distance from the source.

There are some major issues with these assumptions…

In reality, the sensitivity of a loudspeaker varies greatly with drive voltage, frequency, impedance and speaker mounting location. Sadly, many “marketing” specifications greatly exaggerate the sensitivity compared to the real world performance. Physics dictates that similarly sized and priced transducers and cabinets rarely have dramatic differences in sensitivity, so “optimistic” specifications of some models should be viewed with suspicion.

Maximum sound level calculations invariably assume that loudspeaker output is linear over the full power and frequency range, i.e., adding 20 dB more power yields a 20 dB increase in level. Unfortunately, this is certainly not true at all frequencies, and factors like voice coil heating and mechanical displacement limits affect the level and quality at high power. It is important to remember that speaker power ratings are tested to the point of destruction. A speaker on the ragged edge of destruction is not going to sound good. However, low frequency woofers used in cinema subwoofers and screen channel LF systems are usually limited by mechanical displacement long before the thermal power ratings are reached.

It’s important to recognize that the inverse square law is based on a theoretical point source in free field conditions (anechoic), such as outdoors. But a large screen channel speaker does not behave as a point source in the nearfield, and sound level does not continue to fall off in real rooms due to reverberation. QSC recommends using a “loss due to distance (D)” formula based on 15*Log(D) instead of 20*Log(D), which is much more accurate for large rooms such as cinemas. Fortunately, this more realistic approach works in our favor in the real world, since less power is needed than the theoretical Inverse Square Law suggests.

Inflationary Trends

It’s very dangerous to attempt to compare the published specifications provided by different manufacturers. It’s also very dangerous to use those specifications to design cinema sound systems and then make assumptions about the performance of those systems. One problem is that not all manufacturers cite their specification in the same manner, with the same measurement parameters. There are many pitfalls to avoid, but here are three of the most common ones.

1. Publishing numbers with an unspecified frequency range

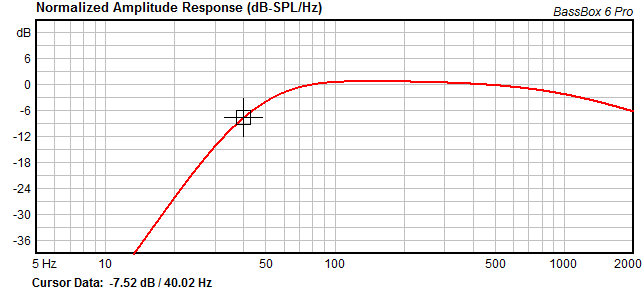
Sensitivity, especially with subwoofers and LF enclosures, falls off at lower frequencies. A sensitivity rating at 200 to 500 Hz for a subwoofer that is used below 100 Hz will give a specification that could be at least 3 to 6 dB greater than reality at those frequencies.

This simulation of the frequency response of a low cost 15 inch woofer shows that 40 Hz is down almost 8 dB from the level we see between 100 to 200 Hz.

2. Ignoring the impedance of the system

Sensitivity is normally stated as the sound pressure level measured at a distance of one meter, on-axis, with a power input of one watt to the driver. As Ohm’s Law tells us, a (nominal) 8 ohm speaker requires 2.83 volts to produce one watt of power, but a 4 ohm speaker requires only 2 volts. 

If a 4 ohm speaker is measured with 2.83 volts, it will actually receive 2 watts of power, and result in an extra 3 dB in the sensitivity specification (2.83V²/4Ω= 2 watts) since twice the power adds 3 dB. This is one of the most common “errors” found in cinema products.

3. Boundary Loading

At low frequencies, a “half space” measurement is typically 3 dB higher than a “whole space” (or free field) measurement, and a “quarter space” measurement is good for an additional 3 dB. If a specification is stated without measurement conditions, be wary! Comparison is only valid if the measurements were made with the same parameters and conditions.

Also, beware of specifications that arbitrarily add 3 dB to the sensitivity of a full-range speaker in half space conditions, since the increase is usually only effective at low frequencies.

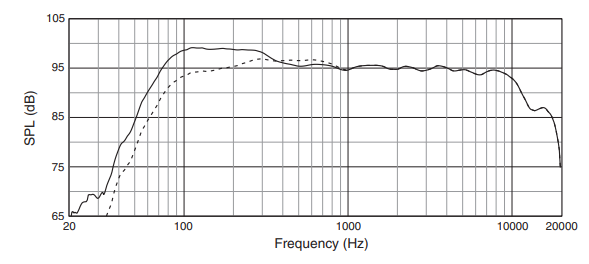
Other than subwoofers placed against a solid wall, or screen channel LF speakers in a properly-built full baffle wall, adding 3 dB for half-space sensitivity is probably wishful thinking. At best, a surround speaker may get a boost below 250 Hz. The graph below is the published frequency response of a competitor’s surround speaker. The solid line is half space (2 pi). By 250 Hz, the advantage over whole space sensitivity (4 pi) has disappeared due to the shorter wavelengths and greater directivity as frequency increases.

It is time re-think the design process

How often do we plug numbers into a spreadsheet calculation for a speaker and amplifier combination with seemingly good results on paper, only to find that the system falls short in the real world? The system may be fine at normal listening levels, but distortion at high levels makes it unpleasant to listen to, or even worse, results in frequent failure. Sadly, this is all too common. Science tells us how to fix this, but the right answers are not always the cheapest solution. HF drivers need to be large and powerful. Speakers must exhibit a well-controlled coverage angle vs. frequency, and maximum power levels should be limited by good sound, not by loudspeaker destruction. 

In a future blog, we’ll look at a real world example, including a deep dive into the design of a screen channel LF speaker to see that sensitivity and thermal power ratings are not a good way to design a great cinema loudspeaker. Stay tuned!